Synthesizer

This week's lab introduces a simple way to synthesize musical tunes. Parts a, b, and c should be done in preparation for your "check-in". The final part is due with the rest of HW # 3.

Caution: Do not use iTunes to play your wav files. iTunes caches audio files, but does not update the cache when the files are changed. Therefore, you are likely to hear old versions of your work when you play updated files with iTunes.

Notice: All code for this lab should be written in pure Python. You can use the math module and the lib6003 library, but not numpy or scipy. You can use matplotlib.pyplot for plotting.

Introduction.

In lecture, we have seen frequency representations of quasi-periodic signals, such as those generated by the musical instruments shown below.

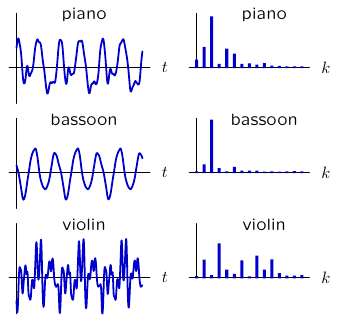
In this lab, we will determine similar harmonic representations of single notes (middle C) from several instruments, and then use that information to simulate a melody played by that instrument.

Part a. Tunes from single sinusoids.

Download this week's code distribution. This distribution contains a skeleton file for this lab (synthesizer.py), as well as recordings of several different instruments playing middle C (C4). The skeleton file contains a description of a tune in the form of a list. Each entry in the list is a tuple of (frequency, duration), where frequency is the fundamental frequency of a note (in Hz) and duration is the length of that note (in seconds).

Write a program to synthesize a .wav file matching this tune by concatenating a sequence of sinusoids with the given frequencies and durations. Use a sampling rate of 44.1kHz, and assume that the tune consists of a sequence of non-overlapping notes, each played one after the other.

Use the lib6003.audio.wav_write function to save result as a .wav file. After you have saved the file, play it back. Do you recognize the tune? You should hear the melody to "Cheap Thrills" by Sia (or, at least, a feeble attempt at it).

Please upload a single .zip file that contains your code and the resulting .wav file:

Select File No file selected

Loading...

Part b. Tune from Fourier Coefficients.

Now assume an instrument that, when playing C4, produces a periodic signal x[n] with the following Fourier coefficients:

Create a version of your tune where every note has this harmonic structure (i.e., if we took any individual note and analyzed it with the proper N, we would find the coefficients listed above).

As an example, we have included this instrument playing C4 as synthetic_C4.wav in the distribution. The notes in your synthesized tune should have the same pitches as the notes in the original, but they should have a similar timbre to synthetic_C4.wav}.

You may find it helpful to note that, for a real valued input, we will always have X[k] = X^*[-k] (so it should not be necessary to loop over all of the coefficients).

Also, the samples you generate should be real valued, even though they're the sum of complex numbers with non-zero imaginary parts. We recommend adding a check for this in your program, which you can do with something like

value = ...
assert abs(value.imag) < 1e-12
samples.append(value.real)

Note: While you are debugging, you might wish to generate only the first few notes of the melody (which should take less time than generating the whole thing).

Please upload a single .zip file that contains your code and the resulting .wav file:

Select File No file selected

Loading...

Part c. Harmonic Analysis of Musical Instruments

In order to synthesize a tune that sounds like a particular instrument, we will need to determine the harmonic structure of that instrument.

Generate a plot of the magnitudes of the first ten harmonics of the oboe. Do the same for the saxophone. Describe the similarities and differences between these series.

Please upload a single .zip file that contains your plots, descriptions, and comparisons:

Select File No file selected

Loading...

Check-In. Before you ask for a check-in, be sure you are prepared to do the following:

• Play the tune that you generated in Part a.
• Play your tune for Part b and describe your method for generating it.
• Describe your plots of the Fourier coefficients of the oboe and saxophone in Part c, focusing on similarities and differences.

Part d. Tunes from Musical Instruments.

Finally, we would like for you to generate three new tunes, playing the same melody as above, but synthesized to sound like three different instruments. Generate one WAV file that sounds like an oboe, one that sounds like a trumpet, and another that sounds like an alto saxophone.

Please upload a single .zip file that contains your code and the resulting .wav files:

Select File No file selected

Loading...

Check In:
Please describe your approach to each of the parts of this lab.

Ask for Checkoff Loading...