Related Transforms
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
Please answer the following questions by entering Python expressions in the box provided. Your answers may contain any of the following:
omegarepresents \omegaOMEGArepresents \Omegasinandcosrepresent \sin(\cdot) and \cos(\cdot), respectivelysqrtrepresents the square root functione,1j, andpirepresent e, j, and \pi, respectivelyReandImrepresent {\rm Re}(\cdot) and {\rm Im}(\cdot), respectively
For this problem, we will consider the following signal f[n], which is known to be zero outside of the range of n plotted below:
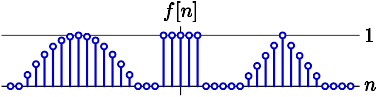
Assume that f[\cdot] has a DTFT given by F(\cdot), such that \displaystyle F(\Omega) = \sum_{n=-\infty}^\infty x[n] e^{-j\Omega n}
For each of the related signals below (each of which is directly related to
f[\cdot], determine its Fourier transform in terms of F(\cdot).
Use F as a Python function in your answers below.
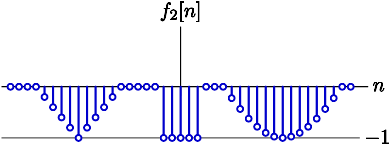
F_2(\Omega) =~
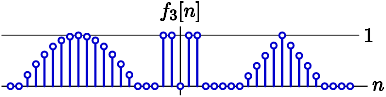
F_3(\Omega) =~
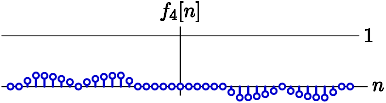
F_4(\Omega) =~
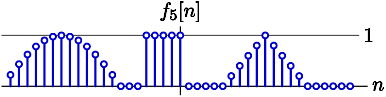
F_5(\Omega) =~
Note that f_6[n] is nonzero over a wider range of n, and that for all n
that are divisible by three, we have the following relationship: f_6[n] = f_6[n-1] = f_6[n+1] = f[n/3]. F_6(\Omega) =~